Example: Basic Run¶
In this example, we will setup a simple parcel model simulation containing two aerosol modes. We will then run the model with a 1 m/s updraft, and observe how the aerosol population bifurcates into swelled aerosol and cloud droplets.
# Suppress warnings
import warnings
warnings.simplefilter('ignore')
import pyrcel as pm
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
Could not find GLIMDA
First, we indicate the parcel’s initial thermodynamic conditions.
P0 = 77500. # Pressure, Pa
T0 = 274. # Temperature, K
S0 = -0.02 # Supersaturation, 1-RH (98% here)
Next, we define the aerosols present in the parcel. The model itself is
agnostic to how the aerosol are specified; it simply expects lists of
the radii of wetted aerosol radii, their number concentration, and their
hygroscopicity. We can make container objects
(:class:AerosolSpecies) that wrap all of this information so that we
never need to worry about it.
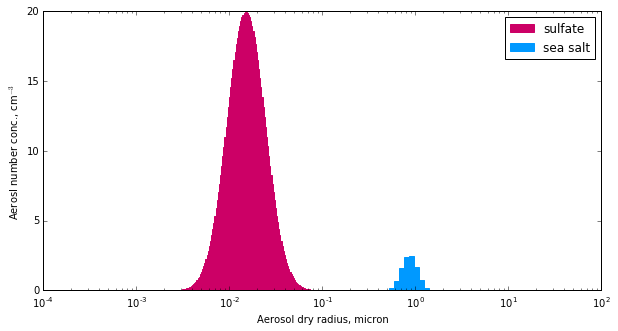
Here, let’s construct two aerosol modes:
Mode |
\(\kappa\) (hygroscopicity) |
Mean size (micron) |
Std dev |
Number Conc (cm**-3) |
|---|---|---|---|---|
sulfate |
0.54 |
0.015 |
1.6 |
850 |
sea salt |
1.2 |
0.85 |
1.2 |
10 |
We’ll define each mode using the :class:Lognorm distribution
packaged with the model.
sulfate = pm.AerosolSpecies('sulfate',
pm.Lognorm(mu=0.015, sigma=1.6, N=850.),
kappa=0.54, bins=200)
sea_salt = pm.AerosolSpecies('sea salt',
pm.Lognorm(mu=0.85, sigma=1.2, N=10.),
kappa=1.2, bins=40)
The :class:AerosolSpecies class automatically computes
gridded/binned representations of the size distributions. Let’s double
check that the aerosol distribution in the model will make sense by
plotting the number concentration in each bin.
fig = plt.figure(figsize=(10,5))
ax = fig.add_subplot(111)
ax.grid(False, "minor")
sul_c = "#CC0066"
ax.bar(sulfate.rs[:-1], sulfate.Nis*1e-6, np.diff(sulfate.rs),
color=sul_c, label="sulfate", edgecolor="#CC0066")
sea_c = "#0099FF"
ax.bar(sea_salt.rs[:-1], sea_salt.Nis*1e-6, np.diff(sea_salt.rs),
color=sea_c, label="sea salt", edgecolor="#0099FF")
ax.semilogx()
ax.set_xlabel("Aerosol dry radius, micron")
ax.set_ylabel("Aerosl number conc., cm$^{-3}$")
ax.legend(loc='upper right')
<matplotlib.legend.Legend at 0x10f4baeb8>
Actually running the model is very straightforward, and involves just two steps:
Instantiate the model by creating a :class:
ParcelModelobject.Call the model’s :method:
runmethod.
For convenience this process is encoded into several routines in the
driver file, including both a single-strategy routine and an
iterating routine which adjusts the the timestep and numerical
tolerances if the model crashes. However, we can illustrate the simple
model running process here in case you wish to develop your own scheme
for running the model.
initial_aerosols = [sulfate, sea_salt]
V = 1.0 # updraft speed, m/s
dt = 1.0 # timestep, seconds
t_end = 250./V # end time, seconds... 250 meter simulation
model = pm.ParcelModel(initial_aerosols, V, T0, S0, P0, console=False, accom=0.3)
parcel_trace, aerosol_traces = model.run(t_end, dt, solver='cvode')
If console is set to True, then some basic debugging output will
be written to the terminal, including the initial equilibrium droplet
size distribution and some numerical solver diagnostics. The model
output can be customized; by default, we get a DataFrame and a Panel of
the parcel state vector and aerosol bin sizes as a function of time (and
height). We can use this to visualize the simulation results, like in
the package’s
README.
fig, [axS, axA] = plt.subplots(1, 2, figsize=(10, 4), sharey=True)
axS.plot(parcel_trace['S']*100., parcel_trace['z'], color='k', lw=2)
axT = axS.twiny()
axT.plot(parcel_trace['T'], parcel_trace['z'], color='r', lw=1.5)
Smax = parcel_trace['S'].max()*100
z_at_smax = parcel_trace['z'].ix[parcel_trace['S'].argmax()]
axS.annotate("max S = %0.2f%%" % Smax,
xy=(Smax, z_at_smax),
xytext=(Smax-0.3, z_at_smax+50.),
arrowprops=dict(arrowstyle="->", color='k',
connectionstyle='angle3,angleA=0,angleB=90'),
zorder=10)
axS.set_xlim(0, 0.7)
axS.set_ylim(0, 250)
axT.set_xticks([270, 271, 272, 273, 274])
axT.xaxis.label.set_color('red')
axT.tick_params(axis='x', colors='red')
axS.set_xlabel("Supersaturation, %")
axT.set_xlabel("Temperature, K")
axS.set_ylabel("Height, m")
sulf_array = aerosol_traces['sulfate'].values
sea_array = aerosol_traces['sea salt'].values
ss = axA.plot(sulf_array[:, ::10]*1e6, parcel_trace['z'], color=sul_c,
label="sulfate")
sa = axA.plot(sea_array*1e6, parcel_trace['z'], color=sea_c, label="sea salt")
axA.semilogx()
axA.set_xlim(1e-2, 10.)
axA.set_xticks([1e-2, 1e-1, 1e0, 1e1], [0.01, 0.1, 1.0, 10.0])
axA.legend([ss[0], sa[0]], ['sulfate', 'sea salt'], loc='upper right')
axA.set_xlabel("Droplet radius, micron")
for ax in [axS, axA, axT]:
ax.grid(False, 'both', 'both')
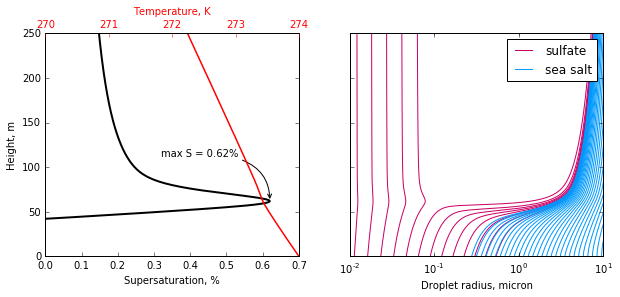
In this simple example, the sulfate aerosol population bifurcated into interstitial aerosol and cloud droplets, while the entire sea salt population activated. A peak supersaturation of about 0.63% was reached a few meters above cloud base, where the ambient relative humidity hit 100%.
How many CDNC does this translate into? We can call upon helper methods
from the activation package to perform these calculations for us:
from pyrcel import binned_activation
sulf_trace = aerosol_traces['sulfate']
sea_trace = aerosol_traces['sea salt']
ind_final = int(t_end/dt) - 1
T = parcel_trace['T'].iloc[ind_final]
eq_sulf, kn_sulf, alpha_sulf, phi_sulf = \
binned_activation(Smax/100, T, sulf_trace.iloc[ind_final], sulfate)
eq_sulf *= sulfate.total_N
eq_sea, kn_sea, alpha_sea, phi_sea = \
binned_activation(Smax/100, T, sea_trace.iloc[ind_final], sea_salt)
eq_sea *= sea_salt.total_N
print(" CDNC(sulfate) = {:3.1f}".format(eq_sulf))
print(" CDNC(sea salt) = {:3.1f}".format(eq_sea))
print("------------------------")
print(" total = {:3.1f} / {:3.0f} ~ act frac = {:1.2f}".format(
eq_sulf+eq_sea,
sea_salt.total_N+sulfate.total_N,
(eq_sulf+eq_sea)/(sea_salt.total_N+sulfate.total_N)
))
CDNC(sulfate) = 146.9
CDNC(sea salt) = 10.0
------------------------
total = 156.9 / 860 ~ act frac = 0.18